sequestering carbon, several books at a time CLII

The latest batch:

review: How to Do Nothing

Jenny Odell.
How to Do Nothing: resisting the attention economy.
Melville House. 2019 

---

This isn’t actually about how to do “nothing”: it’s about how to do something meaningful, rather than the nothing that results from being trapped in the shallows of social media and “the attention economy”, of consumerism and incessant productivity. It’s about how to disengage from that time-suck, and how to use the resulting time beneficially.

The argument goes something like this. The attention economy is bad for us: it grabs our attention but doesn’t give anything in return; it’s like junk food engineered for craving more rather than providing nutrition. However, we can’t just walk away from the world and become a hermit: we need some contact with it to function, to keep in touch, to do our work; we are social beings. So we need to “resist in place”: do what is needed, but no more. This is of course difficult, because the digital world is engineered to make it hard to ignore; consumerism is the way our world current runs; not everyone has the resources to just stop.

Odell suggests that one way to resist is to pay “deep attention”, to go down rabbit holes. Rather than skimming over the surface glitter, dig down in one place, and notice, and think. The approach that worked for her stemmed from bird watching. Initially this was paying enough attention to distinguish species; this led to noticing where and when they turned up. From there, it was a short step to thinking about the plants and the local ecology, and further. She describes the experience as “re-rendering” her reality, seeing the world in a new, different way. Ecology is about networks, flows, and a lack of sharp, easily defined boundaries; this less sharply-defined reality needs extra attention and effort to see.

Odell suggests that deep connection with the natural world is what is needed. However, I think many more things are sufficiently fractal to work: you can pay attention and dig deep and discover more and more wherever you start: probably any initial hobby or interest can lead to ever-increasing depth and richness: from birds to ecology; from sport to physiology or economics or equipment design; from crafting to materials engineering and science, or supply chains, or sustainable raw material production; and so on. Indeed, Odell uses discovery of this ever deepening complexity and context as evidence we do not live in a context-free simulation:

[p126] Unlike the manufactured Main Street Cupertino, [the creek] is not there because someone put it there; it is not there to be productive; it is not there as an amenity. It is witness to a watershed that precedes us. In that sense, the creek is a reminder that we do not live in a simulation—a streamlined world of products, results, experiences, reviews—but rather on a giant rock whose other lifeforms operate according to an ancient, oozing, almost chthonic logic. Snaking through the midst of the banal everyday is a deep weirdness, a world of flowerings, decompositions, and seepages, of a million crawling things, of spores and lacy fungal filaments, of minerals reacting and things being eaten away—all just on the other side of the chain-link fence.

Odell finishes by talking of what comes next, after this deep attention has brought (in her case) the ecology front and centre. This ecology has been damaged, and is in need, not necessarily of restoration to some previous supposedly pristine state, but certainly of remediation, to a better, more healthy state. This requires seeing the complexity of what was there originally, and working with that complexity, in a form of “patient collaboration”. This work has no endpoint; it is a process of becoming.

I was surprised to find this turned into a book about the complexity of ecology, so soon after having read What Should a Clever Moose Eat?. They make a good pair. Even it you don’t want to turn your attention to ecology, but rather start with some other hobby or topic of choice, there is a lot to think about in this discussion. Stop consuming digital junk; pay attention to your mental nourishment!

---

For all my book reviews, see my main website.

UCNC day 3

Midway through the week-long UCNC conference, today we had two great talks, a group photo, and the conference outing.

First up, Mika Hirvensalo gave a (remote) presentation on "41 years of quantum computing" as an introduction to the QC workshop to come on Friday.  The "41 years" refers to Feynmann's 1982 paper of simulating quantum physics.  Of course, quantum mechanics itself is somewhat older than that, but Feynmann was arguably the first to consider it as the basis for a computational use.  Mika's talks covered a variety of historical themes: quantum computing itself, from von Neumann's (pre-Shannon) definition of quantum entropy, via Feynmann, the Deutsch and Shor algorithms, and more recent work on quantum complexity theory; some pre-history of quantum physics itself, starting with Young's two slit experiment; and practical milestones in building (small, noisy) quantum computers, from 2 bit NMR, via ion traps and photons, D-Wave's annealer, to qubit circuit machines.  A fascinating perspective.

Next up, Lila Kari gave a keynote on using mathematical analyses of DNA sequences to investigate environmental adaptations of extremophile genomes.  There was a lot of fascinating detail here about the biology of the bugs, and how to analyse them.  I really loved the use of the "chaos game" algorithm to turn a genome sequence into a 2D fractal plot, where differences and similarities are clearly apparent on visual inspection.

We moved outside into the warm Florida sunshine for a photograph. (The locals kept apologising for the bad weather: although it was sunny, it was "only" in the low 20s (Celsius), which as far as I was concerned is perfect weather!)  In olden days a conference photograph was a formal affair, all lined up with a proper photographer taking the picture.  Nowadays, loosely group everyone on a convenient staircase, snag a passer-by to be the photographer, and snap a few pictures on a smartphone.

Then off to the conference outing, to the "old" town of St. Augustine.  The campus is deserted this week, because it is spring break; St Augustine was packed, for similar reasons.  But we had a good walk round, enjoying the old town (which looked suspiciously new in places), the fort, the shore, and some key lime pie.

the old fort

panoramic view: there were fewer people here, probably because it was quite breezy and nicely cool

a view across the bay

trees in the town centre, draped in Spanish moss; beautiful

the Buddhabrot

As we have seen, the Mandelbrot set can be calulated by iterating a function, and testing whether the sequence it generates diverges or not.  The so-called Buddhabrot (named for its appearance) looks at the trajectory of the generated sequence, as the generated points hop about, diverging or not. Points that start with a \(c\) value outside the Mandelbrot set, and so produce diverging sequences, may nevertheless have points along the way that land inside the set.

The Buddhabrot takes all the points ourside the set, and plots each point in the trajectory to divergence.  This leads to a density map: some points are visited more often than others (it is conventional to plot this rotated 90 degrees, to highlight the shape):

42 million randomly chosen values of \(c\)

In addition, there is the anti-Buddhabrot, which plots the trajectories of all the \(c\) values inside the Mandelbrot set.  These do not diverge: some converge inside the set, others cycle around.

Again, the code is relatively simple, and you can calculate the Buddhabrot and anti-Buddhabrot at the same time:

import numpy  as np
import matplotlib.pyplot as plt

IMSIZE = 2048 # image width/height 
ITER = 1000

def mandelbrot(c, k=2): 
    # c = position, complex; k = power, real
    z = c
    traj = [c]
    for i in range(1, ITER): 
        z = z ** k + c 
        traj += [z]
        if abs(z) > 2: # escapes
            return traj, []
    return [], traj
    
def updateimage(img, traj):   
    for z in traj:
        xt, yt = z.real, z.imag
        ixt, iyt = int((2+xt)*IMSIZE/4), int((2-yt)*IMSIZE/4)
        # check traj still in plot area
if 0 <= ixt and ixt < IMSIZE and 0 <= iyt and iyt < IMSIZE:   
            img[ixt,iyt] += 1    

# start with value 1 because take logs later
buddha = np.ones([IMSIZE,IMSIZE]) 
abuddha = np.ones([IMSIZE,IMSIZE]) 
for i in range(IMSIZE*IMSIZE*10):
    z = np.complex(np.random.uniform()*4-2, np.random.uniform()*4-2)
    traj, traja = mandelbrot(z, k)
    updateimage(buddha,traj)
    updateimage(abuddha,traja)
                
buddha = np.square(np.log(buddha)) # to extend small numbers
abuddha = np.log(abuddha)          # to extend small numbers

plt.axis('off')
plt.imshow(buddha, cmap='cubehelix')
plt.show()    
plt.imshow(abuddha, cmap='cubehelix')
plt.show()

These plots are more are computationally expensive to produce than the plain Mandelbrot set plots: it is good to have a large number of initial points, and a long trajectory run.  There are some beautifully detailed figures on the Wikipedia page.

As before, we can iterate using different powers of \(k\), and get analogues of the Buddhabrot.

\(k = 2.5\), the "piggy-brot"

More figures and animations of the Mandelbrot set, the Julia set, and the Buddhabrot, are available on my website.

Julia set

Before the Mandelbrot set came the closely related Julia set.

Consider the sequence \(z_0=z; z_{n+1} = z_n^2 + c\), where \(z\) and \(c\) are complex numbers.  Consider a given value of \(c\).  Then for some values of \(z\), the sequence diverges to infinity; for other values it stays bounded.  The Julia set is the border of the region(s) between which the values of \(z\) do or do not diverge.  Plotting these \(z\) points in the complex plane (again plotting the points that do diverge in colours that represent how fast they diverge) gives a picture that depends on the value of \(c\):

\(c = -0.5+0.5i\), a point well inside the Mandelbrot set

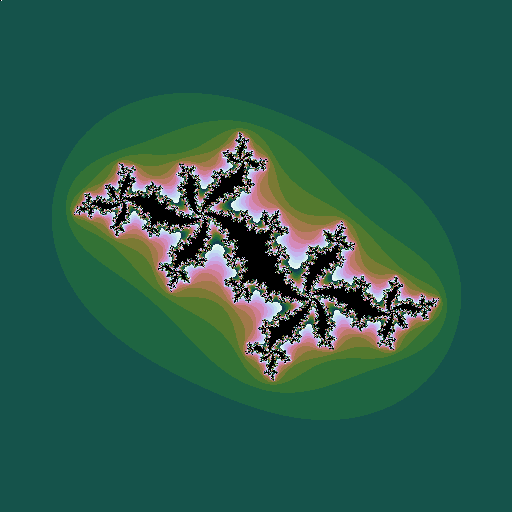\(c = -0.5+0.6i\), a point just inside the Mandelbrot set

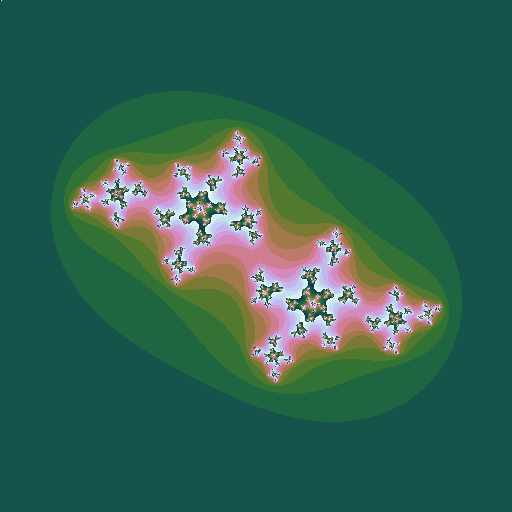\(c = -0.5+0.7i\), a point outside the Mandelbrot set

If the point \(c\) is inside the Mandelbrot set, the corresponding Julia set is one connected border around one connected region.  If it is outside, there are instead many disconneted regions.  The deeper inside the Mandelbrot set, the larger and rounder the black region in the Julia set looks; the further outside the Mandelbrot set, the smaller and hence paler he Julia set looks.

This leads to the idea of plotting the Mandelbrot set in a rather different way.  For each value of \(c\), instead of plotting a pixel in a colur representing the speed of divergence, plot a little image of the associated Julia set, whose overall colour is related to the speed of divergence:

Julia sets mapping out the Mandelbrot set

As with the Mandelbrot set, we can construct related fractals by iterating different powers, \(z_0=z; z_{n+1} = z_n^k + c\):

\(k=3, c = -0.5+0.598i\)

\(k=4, c = -0.5+0.444i\)

The code is just as simple as, and very similar to, the Mandelbrot code, too:

import numpy  as np
import matplotlib.pyplot as plt

IMSIZE = 512 # image width/height 
ITER = 256

def julia(z, c, k=2): 
    # z = position, complex ; c = constant, complex; k = power, real
    z = z
    for i in range(1, ITER): 
        z = z ** k + c 
        if abs(z) > 2: 
            return 4 + i % 16 #16 colours
    return 0
    
julie = np.zeros([IMSIZE,IMSIZE]) 
c = np.complex(-0.5,0.5)

for ix in range(IMSIZE):  
    x = 4 * ix / IMSIZE - 2
    for iy in range(IMSIZE):
        y = 2 - 4 * iy / IMSIZE
        julie[iy,ix] = julia(np.complex(x,y), c, 5)
        
julie[0,0]=0   # kludge to get uniform colour maps for all plots

plt.axis('off')
plt.imshow(julie, cmap='cubehelix')
plt.show()

Mandelbrot set

When I reviewed Matt Pearson's Generative Art, and plotted a Mandelbrot set made from random splodges, I went and looked at my own webpage about this structure.  I discovered a case of bit rot: the little Java applet I'd written many years ago had stopped working, as is the way with much old software.  Rather than rewrite it, I pottered around in Python, reproducing some of the plots.

The Mandelborot set is a highly complex fractal generated from a very simple equation. Consider the sequence \(z_0=0; z_{n+1} = z_n^2 + c\), where \(z\) and \(c\) are complex numbers.  For some values of \(c\), the sequence diverges to infinity; for other values it stays bounded.  The Mandelbrot set is all the values of \(c\) for which the sequence does not diverge.  Plotting these points in the complex plane (and plotting the points that do diverge in colours that represent how fast they diverge) gives the now well-known picture:

If \(z\) is raised to a different power, different sets are seen, still with complex shapes.

iterating \(z^4 + c\)

The power doesn't even need to be an integer.

iterating \(z^{2.5} + c\)

The discontinuities visible are due to the fractional power resulting in a logarithm in the solutoin, which is multi-values in the complex plane. The plot shows only the principal value.

We can make an animation of the shape of the set as this power \(k\) changes:

\(k = 1 .. 6\), step \(0.05\)

One thing I love about the Mandelbrot set is the sheer simplicity of the code needed to plot it:

import numpy  as np
import matplotlib.pyplot as plt

IMSIZE = 512 # image width/height 
ITER = 256

def mandelbrot(c, k=2): 
    # c = position, complex; # k = power, real
    z = c
    for i in range(1, ITER): 
        if abs(z) > 2: 
            return 4 + i % 16 #16 colours
        z = z ** k + c 
    return 0  

mandy = np.zeros([IMSIZE,IMSIZE]) 
for ix in range(IMSIZE):
    x = 4 * ix / IMSIZE - 2
    for iy in range(IMSIZE):
        y = 2 - 4 * iy / IMSIZE
        mandy[iy,ix] = mandelbrot(np.complex(x,y), k)
        
    plt.axis('off')
    plt.imshow(mandy, cmap='cubehelix')
    plt.show()

And there's more.  But that's for another post.

sequestering carbon, several books at a time XCI

The latest batch, pre Christmas rush:

next step on from spokes rotating backwards

Blooms are strobe-animated sculptures

---

For all my social networking posts, see my Google+ page

sequestering carbon, one Christmas at a time IV

Here’s the books we got each other for Christmas.  Lots of fun reading for the New Year!

UCNC day 2

UCNC day 2, a full day of talks.

First up was Masami Hagiya with an invited tutorial on “Gellular Automata”. These are a form of cellular automata implemented using gels and chemical reactions. The walls between cells can be “decomposed” or “composed” using chemical reactions – or instead can “swell” or “unswell” forming a valve. This allows chemicals to move between cells. There are theoretical results demonstrating these systems can in principle implement certain kinds of CAs. The tutorial moved on to talking about implementations. Most of the manipulations involve a form of DNA chemical computing: using complementary strands to form networks of polymers, or to control diffusion by attaching anchors. These processes can be controlled by the DNA technique of “strand displacement” that breaks the bonds between the complementary strands. There are some initial prototype implementations. These are still rather complicated, needing multiple chemical species to implement relatively simple state transitions. However, it is early days yet, and more efficient approaches may well be discovered.

Next was the workshop on Membrane systems (mostly P-Systems). Rudolf Freund started off with a tutorial, helping to introduce the concepts to people not that familiar with the area. Then on to the technical talks, covering a wide set of membrane computing topics.

Finally was the afternoon technical session. We started with a talk on Affine Automata: these use an underlying logic that is partway between classical probabilistic automata and quantum automata. Next was a talk about languages (sets of strings) arising from finite walks on Sierpinsky gaskets. And finally we had a talk on Matrix Ins-del (insertion deletion) systems (although I think a better name would be List Ins-del systems). These three combined nicely as a range of different ways of looking at language (in the CS sense) recognisers.

Then off to The Great Wall Chinese restaurant, for a very nice duck in ginger.

Mandelbulb rocks

Three minutes of complex fractal beauty.

View full screen for best effect.


[via BoingBoing]

---

For all my social networking posts, see my Google+ page

swirl, pop, cut

Complex and complicated

an experimental dreamlike video rocking us smoothly through circular moves

The Colors of Feelings from Thomas Blanchard on Vimeo.

I don’t find it particularly dreamlike or smooth: the cuts are way too frequent.  Just as I’m falling into the swirls … bam! another cut.

But fascinating and beautiful, nonetheless

[via BoingBoing]

---

For all my social networking posts, see my Google+ page

Inception

It’s enclaves all the way down!

I’d heard this border dispute was being settled, and thought I understood the problem – little pockets of India in Bangladesh, and vice versa.  I hadn’t realised that it included an enclave surrounded by an enclave surrounded by an enclave surrounded by another state

someone who lived in an enclave would need a visa to enter the foreign country that surrounded the enclave. However, the only way to get that visa was to travel to a major city in the main body of their country, something that was impossible without illegally entering the foreign country.

---

For all my social networking posts, see my Google+ page

petrified lace

Some friends from LA who are in the UK for a while visited us toady.  We took them to Ely Cathedral.  I’ve been there once before, albeit about 35 years ago, while it turned out that one of our visitors had been there a fortnight ago!  Nevermind, it’s spectacular, and there’s plenty to see.

Ely cathedral, in sunlight

The famous central Octagonal Tower

The decorated ceiling of the nave.  The lines across it are Christmas lights!

The view back down the aisle

Sunlight through stained glass

Co-opted pagan symbolism

Looking up into the Octagonal Tower

Superb stained glass: we need a camera with better dynamic range to do it justice.

"Seated one day at the organ, ..."

Bishop Peter Gunning looking very relaxed.

An explosion of fractal lacework in stone.

And that’s just a small sample: there’s the wonderful wood carving in the choir, the bright and airy Lady Chapel, the wrought iron staircase up to the pulpit, and more.

We also visited the Stained Glass Museum (no photography allowed), which had lots of interesting exhibits and history.

Well worth a visit.

soap opera

The third day in the hotel in Lyon, and the third cake of foil-wrapped soap appears in the bathroom.  It’s not a small cake, either:

toothbrush shown for scale

That’s a lot of soap.  Where does it all go?

And no, I don’t know what’s up with the psychedelic sink surround, either.  It looks like the death throes of some complex reaction-diffusion system.  Is bonkers bathroom design a feature of Lyon hotels?

Processing Mandelbrot

I’ve just started playing with Processing and processing.js

It’s a straightforward way to build interactive graphics. I’m trying it out on that old stalwart: the Mandelbrot set.

It’s a bit slow in a browser (as it’s interpreted JavaScript, not compiled Java), but still very cool.

Processing is a dreadful name for googling for help…

screenshot

---

For all my social networking posts, see my Google+ page

Bees and Bombs and Gifs

The Bees and Bombs tumblr shows great geometrical gifs.

(found via BoingBoing)

---

For all my social networking posts, see my Google+ page

Fractal Experience

Eric Soderberg’s project.

(via BoingBoing)

---

For all my social networking posts, see my Google+ page

insane detail

Another amazing zoom, here of a detailed fractal landscape.  It not only has insane detail, but it is dynamically changing!  Some people clearly have way too much computing power on their hands…

   

 (via BoingBoing)

---

For all my social networking posts, see my Google+ page

the chaos game

By iteratively applying specific sets of transformations to the unit square, we can generate fractals.  For example, the famous Sierpinski triangle can be generated from three simple transformations:

Three transformations (shown in black, red, green), shown by their action on the unit square (grey), produce the Sierpinkski triangle

Rather than iteratively transforming shapes (the base Iterated Function System approach), these plots are produced using the “chaos game” algorithm: start with a random point, and plot its position as it is successively transformed by a random choice of transformation:

x := rnd
repeat
   choose transform w_i with probability p_i
   x := w_i(x)
   plot x

The resulting plot converges to the relevant fractal.

Different sets of transformations give different fractals.

Here, the black and green transformations are as before, but the red transformation includes a rotation

One nice feature of this approach is that smoothly changing the transformations smoothly changes the fractal.

Of course, there can be more than three transformations:

A pentagonal fractal produced by five transformations

The transformations don’t all have to have the same scale factors:

A “snowflake” produced from four transformations, one with a smaller "shrinkage" than the others

This is where the probabilities in the algorithm come into play.  When all the transformations have the same scale factor, we can choose transformations with a uniform random distribution.  When different scale factors are used together, a good heuristic is to choose transformations with probabilities weighted by the area of the relevant transformed square (given by the determinant of the transformation matrix).

The transformations don’t actually have to be squares: we can have different scalings in different directions, and shears, giving more complicated looking fractals:

A “coral tree”

And then we can smoothly transform between quite dissimilar fractals, by linear interpolation between their transformation sets:

From pentagon to coral, and back.

Probably the most famous fractal of this form is the “Barnsley fern”.

What is marvelous for playing about with these systems is that the plots can be produced with very little code: the code to define the transforms, plot the points, and construct the animated gifs, outweighs the core of the chaos game algorithm itself.